Health Tips

home . Health Tips


The Optic Disc as the Basis for Effective Treatment of Glaucoma

Dr.Rezaul Murshed
 M.B.B.S(D.M.C).D.O(D.U)
AHMAD MEDICAL CENTER LTD
71, Dhanmond Residential Area
Road.#15A, Dhaka-1209
Cell: 0171-533357 Res: +880-2-8152761


Optic Disc

  • Evaluation of the Optic Nerve is at
  • The HEART of the
  • Diagnosis and Management
  • GLAUCOMA

    • Optic Nerve Examination

  • Why Examine?
  • The tissue at issue
  • Glaucoma Usually has a Characteristic feature- Cupping
  • Can have other associated findings Disc Hemorrhage Rim thinning/pallor/or notching Vascular alterations

    • Optic Nerve Characteristics

  • Disc area ranges from 0.8 mm ² to 6mm²
  • Disc area is independent of age beyond about 10 years
  • Larger people (men, tall people) probably have larger nerves
  • Disc area is certainly larger in myopes, smaller in hyperopes
  • Varies by race Black>Hispanic>Asian>White
  • Larger discs have larger neuroretinal rim area and more nerve fibers and less "Crowding" of nerve fibers

    • Optic Nerve Size and Glaucoma

  • Larger nerves may be at higher risk for glaucoma --Black -- NTG has been reported in larger nerves
  • Mechanism may be due to more displacement of lamina by IOP
  • Smaller nerves may be at higher risk for glaucoma --Fewer axons, so less "reserve" supply --Crowding may make any laminar bowing more likely to cause damage

    • The Normal Nerve - Neuroretinal Rim Shape

  • Disc is vertically oval, cup is horizontally oval

    • --The ISNT rule (Jost Jonas)
    --Thickest rim Inferiorly > Superiorly > Nasally > Temporally (Thinnest)
    --Critical to examine in early glaucoma


    SIMPLE DRAWING


    I:S = 2:1.5, N:T= 2:1

    Neuroretinal Rim Shape and Glaucoma

  • Glaucoma causes diffuse damage to the rim with some preferential spots

    • --First loss is typically inferotemporal and then superotemporal
    --For more advanced disease temporal regions are more thinned
    --For very advanced disease typically the nasal rim is the thickest remaining part (superonasal thicker)

  • This loss matches visual field defects

    • --Typically affect upper nasal quadrant first
    --Then inferior field and so on
    --End stage disease often has only a inferior temporal island left (superonasal rim)

  • Why does damage occur in this way?

    • --Larger and more laminar pores at the poles might be important
    --Laminar bowing is more prominent at the poles
    --Axons are more kinked at the disc periphery


    Advance glaucoma


    This school teacher of 45yrs. enjoys 6/4.5R/E&; 6/6 L/E. Binoculr Esterman shows 4 adjacent scotoms in the


    Sup. Field & 6 scotomas seen in the lower Temp. zone. Here out of 120 points, he can see 109 & cannot See 11 points. When not seen crosses 10>in screening test than full Threshold test to be done. This is an advance case of POAG R>L.

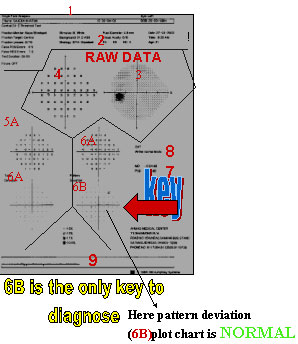
    DENSE SUP ARCUATE SCOTOMA


    DENSE SUP ARCUATE SCOTOMAS EMANTING FROM THE BLIND SPOT JOINS THE SUP ARCUATE SCOTOMA LATER JIONS THE NASAL SUP NASAL STEP.FIELD MATCHES WITH THIN INF NRR.A CASE OF ESTABLISHED POAG.

    DISC SHOWS NO INFERIOR NEURO RETINAL RIM

    NORMAL NERVE-NRR SHAPE

  • DISC IS VERTICALLY OVAL V>H
  • CUP IS OVAL HORIZONTALLY H>V
  • THE ISNT RULE
  • THICKEST RIM INFERIORLY>SUPERIORLY>NASALLY > TEMPORALLY(THINNEST) ISNT
  • CRITICAL TO EXAMINE IN EARLY GLAUCOMA

    • Asymmetric DISC

    Tissue between The cup & disc is NRR made of nerve & capillaries So, looks red to orange



    NRR

  • NRR COLOR IS FROM PINK RED TO ORANGE
  • RIM PALLOR > CUPPING = NEURO DISEASE
  • RIM PALLOR & CUPPING = GLAUCOMA
  • IF ANY ONE CAN DIAGNOSE THE NRR / NFLD IS THE KEY TO DIAGNOSE OF THE CASE

    • Cup size and Disc Size

  • Large nerves have large cups but normal rims
  • Small nerves often have no cup -- Cupping in a small nerve (even a small cup/disc ratio) might be pathologic Look for peripapillary abnormalities too
  • Progressive enlargement of the cup is a hallmark of glaucoma
  • Really thinning of the rim
  • Overall disc gets pale, vessels thin, cup depth increases and cup area increase
  • Normal c/d ratio range from 0.0 to 0.9

    • Optic Nerve Head Cupping is a Unifying Feature of all GLAUCOMAS


    Cupping



    Enlargement of cup / loss of Neuroretinal Rim

    Disc Examination

  • DISC EXAMINATION BY AN EXPERIENCED GLAUCOMA SPECIALIST WAS ACCEPTED AS GOLD STANDARD

    • OLD IS GOLD

    Optic Nerve Examination Problems

  • Variable inter-observer agreement
  • Physiological Cupping Variation
  • Variable cupping patterns can not be quantified readily by a simple cup/disc ratio

    • HORIZONTAL C:D 0.4, CUP OCCUPIES 4/10 WIDTH OF DISC "Armaly"


    Problems with Armaly's c/d

    Healthy Disc

    c/d 0.5
    Normal Field

  • Where the cup is located?
  • No disc size
  • No regards to RIM

    • Sick disc

    c/d 0.5
    Field defect


    Disc Size

    Small disc

    1.0 mm
    c/d 0.2Disc Size <1.3mm

    Large disc


    2.Omm
    c/d 0.6 Disc size 2mm


    Here Smaller disc is more damaged

    Determine Thinnest Rim/Disc

    Ratio

    Rim Disc/Disc 0.2
    Here thinnest rim .2mm & if disc size 1 than Rim/Disc = 0.2
    Normal field



    Rim less than <45
    Field defect


    Optic Nerve Examination Problems





    Which of these nerves is more likely Pathologic?


    The Disc Damage likelihood Damage Scale (DDLS)

  • The Disc Damage Likelihood Scale is a method of estimating the amount of damage that has occurred to the optic nerve based on one consideration, specifically, the width of the tissue ( rim ) that is made up of the living nerve fibers that pass from retina, through the optic nerve, back into the brain. Or, if that tissue ( rim ) is absent, the extent of its absence.

    • Spaeth G & Henderer J 2002 May


    The Disc Damage Likelihood Scale (DDLS)

  • Use knowledge of disc size (vertical disc diameter) to stage disc damage according to rim thickness
  • Nerve diameter usually 1.0-2.0 mm
  • Rim/disc ratio
  • Ten stage scale
  • Based on clinical examination

    • Comparison of cup/disc and Rim/Disc ratio


    Cup/Disc = 0.1
    Rim/Disc = 0.45


    C/Disc = 0.3
    Rim/Disc = 0.35


    Cup/Disc = 0.8
    Rim/Disc = 0.1


    Cup/Disc = 0.9
    Rim/Disc = 0.05


    When disc is arbitrarily Considered 1


    BY SLIT LAMP

  • Vertical Slit beam to create rectangle of light
  • Beam 1/4 to 1/3 of size of disc diameter wide
  • Adjust length of beam to match vertical "height" of the disc
  • Example
    • BAYER is the lead author and he is the first publication of the scale

    Conversion Chart

    Manufacturer LENS
    60D 78D 90D
    VOLK 0.88 1.11 1.33
    NIKON 1.03 1.63
    Lim, et al. J Glaucoma 1996; 5:241

    Measuring Disc Diameter

  • Read length of light column from the continuous scale on the slit lamp
  • Multiply this length by a conversion factor

    • -L ens specific
    - Manufacturer specific


    Example
    1.6mm(Vertical length)x1.11(Volk 78)=1.78mm, will be the disc diameter.


    How to determine the rim/disc ratio


    So, rim/disc=.35/1.78=0.19
    Stage 2

    When damage will occur

  • Small disc 1 rim 0.1 r/d=0.1(damage disc)
  • Large disc 2 rim 0.2 r/d=0.1(normal disc)
  • In small disc damage will occur when r/d <0.2 & in large disc damage will occur r/d<0.1

    • Theoretical R im Area by Optic Nerve Diameter

    Henderer 2000


    Estimation of Disc Pathology by Rim/Disc ratio


    DDLS STAGING



    a is a healthy optic disc, DDLS Stage Oa, rim/disc .4
    b is a possible disc damage DDLS Stage 2, rim/disc .25
    c is a severely damaged optic disc,stage 7a, no rim From 9.30 to 5.30

    Staging of DDLS

  • Oa-No narrowing of the rim at all
  • 3-One area rim is extremly narrow one can barely see it
  • 4-Rim less than 1/8 of circumference of entire rim
  • 5-One portion of NRR loss
  • 7-3/4 of the of the entire rim is lost

    • The Disc Damage Likelihood Damage Scale

    STAGE
    		Narrowest Width of rim or Circumferential no rim
    0 0.3-0.5
    1 0.2-0.29
    2 0.1-0.19
    3 0.01-0.1
    4 No rim <45 °
    5 No rim 45°-90°
    6 No rim 91°-180°
    7 No rim > 180°


    DDLS Conclusions

  • Simple Opthalmoscopic Examination
  • Slit Lamp with +78D,+90D
  • Simple Disc Drawing with pen, 5 min
  • Based on clinical examination
  • A quantitative method of assessing optic nerve damage
  • Diagnosing, Staging and Monitoring of Glaucoma

    • DDLS not the Key

  • DDLS is not really the key
  • Look for disc size
  • Focus on the rim all along 360 °
  • No CUP any more Recall the ISNT rule

    • PROVIEW TONOMETER